- 0120-19-71-48平日 15:00~22:00
土曜 13:00~20:00 - お問合わせ
- 0120-19-71-48平日 15:00~22:00
土曜 13:00~20:00 - お問合わせ
東大寺学園中学校 2016年 大問2(場合の数)
規則に従って数字を並べる問題です。
(1)、(2)がそれぞれ次の問題へのヒントになっています。
(3)は樹形図をかくと解きやすいですが、全部をかくのではなく
わかっている部分をできるだけ省略するとあまり手間をかけずに済みます。
問題
3種類の数字1, 2, 3を次の規則①, ②, ③にしたがって,左から順に一列に並べます。
規則① 1の次は3
規則② 2の次は2または3
規則③ 3の次は1または2または3
例えば,2個の数字を並べるとき, 13, 22, 23, 31, 32, 33の6通りの並べ方があります。このとき,次の問いに答えなさい。
(1) 4個の数字を並べるとき,左から1番目と4番目が2である並べ方は全部で何通りありますか。
(2) 10個の数字を並べるとき,左から1, 4, 10番目が2で左から7番目が1である並べ方は全部で何通りありますか。
(3) 10個の数字を並べるとき,左から1, 4, 10番目が2である並べ方は全部で何通りありますか。
解説
各規則を整理すると、左の数字と右の数字の並べ方は下表のようになります。
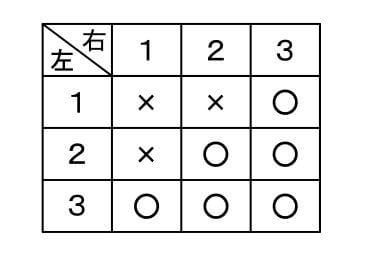
(1) 使う数字が決まっている場所の隣は、使える数字が限られます。
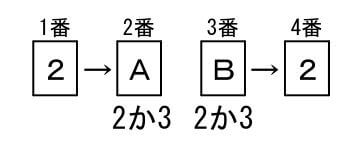
A=2か3、B=2か3が使えます。また、ABの並べ方は2、3を使った全ての並べ方が可能です。
よって4個の数字の並べ方は、1×2×2×1=4通り
具体的なABは22, 23, 32, 33です。
(2) 1の左右は3に限られますので、6番目と8番目は3になります。
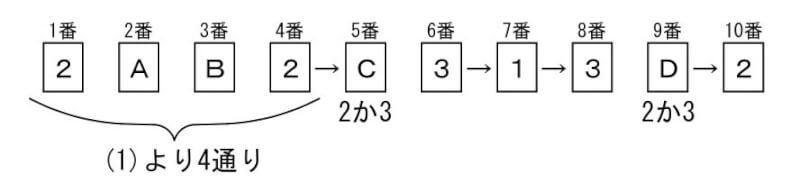
C=2か3、D=2か3が使えますので、10個の数字の並べ方は(1)の結果も利用し、
4×2×1×1×1×2×1=16通り
(3) (2)のときから、5~9番目の数字を新たに検討する必要があります。
左右の数字次第で、各数字が使えるときがあれば使えないときもありますので、樹形図をかいて整理します。
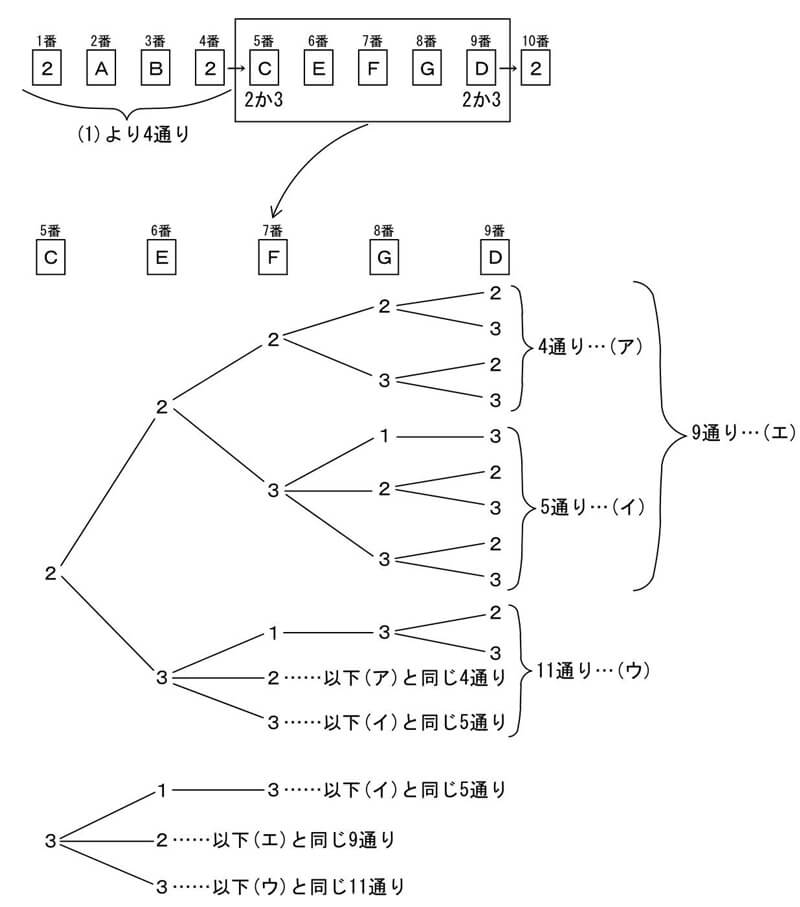
5~9番目の並べ方は9+11+5+9+11=45通りあります。
したがって、全ての並べ方は、4×45×1=180通り
5~9番目の並べ方は別の方法でも求められます。
大きくは、1を使わない場合と使う場合に分けます。
【1を使わない場合】

【1を使う場合】…3, 1, 3を一つの塊として考えます。
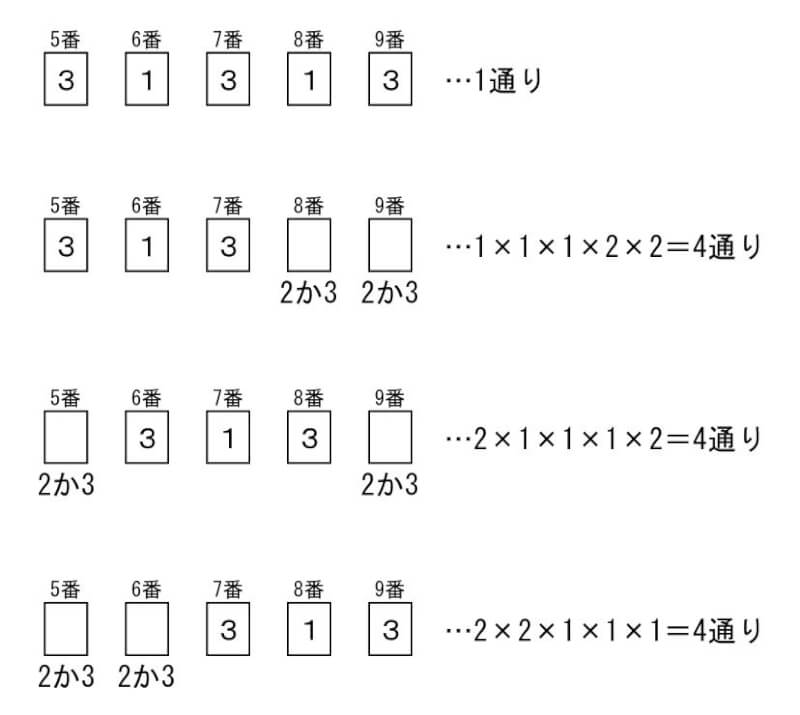
32+1+4×3=45通り、となります。





