灘中学校　2020年　第２日大問４　（平面図形）

難関校では対策必須の作図問題で、円が平行移動します。
（1）は昭和63年度に洛星中で同様の問題が出されています。
細部を見落とさないよう、注意深く精密に作図する必要があります。

問題

平面上に、１辺の長さが6cmの正三角形ＡＢＣと、半径が6cmの円の形をした輪があります。

輪ははじめ右の図のように置かれていて、輪の中心は点Ｂと重なっています。

次のように輪を平面上で移動させるとき、輪が通過する部分の面積をそれぞれ求めなさい。

ただし、輪の太さは考えないものとします。

また、円周率を3.14とし、三角形ＡＢＣの面積を15.59㎠とします。

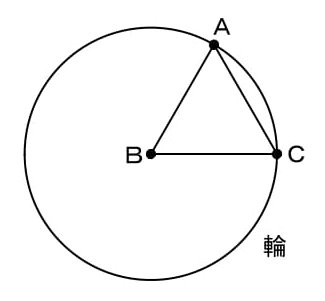
灘中の2020年入試算数

（1）輪の中心が、辺ＢＣ上をＢからＣまで動く。

（2）輪の中心が、辺ＡＢ上をＢからＡまで動いたのち、辺ＡＣ上をＡからＣまで動く。

注…本解説では円周率（3.14）をπとしています。

（1）作図のコツですが下図のように赤線部分が作る部分と青線部分が作る部分に分けて考えるとよいです。

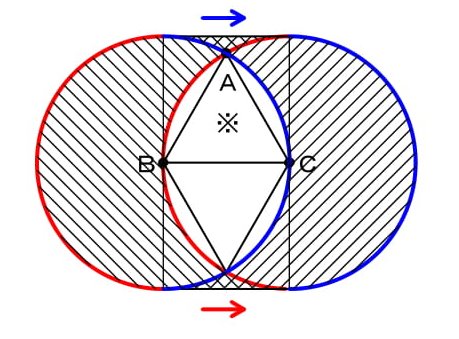
※印の正方形について、各部分の面積を求めておきます。これらの数値は（2）でも使います。

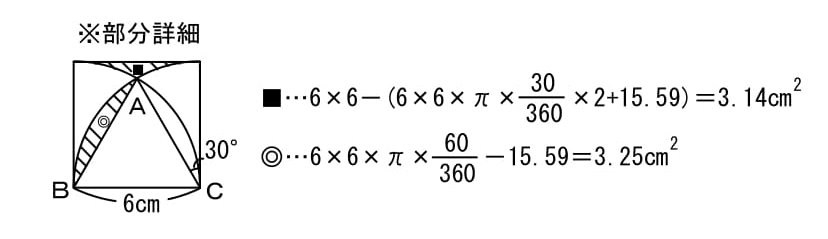
半円２つと長方形を足し、中央部分を引きます。

（2）（1）同様に作図すると以下のようになります。中央部に空白部分ができます。

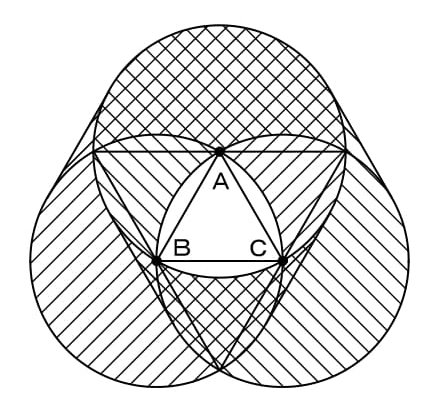
求積する部分ごとに分けると次のようになります。

[blogcard url=”https://iriejuku.jp/kakomon/”]