東大寺学園中学校　2022年　大問３(速さ、平面図形)

2022-02-11 入試算数　「この一題」

速さをメインテーマとしつつ、平面図形の要素も取り入れられたユニークな問題です。
太陽光による影が関係してきますが、速さの問題として考えたことと、平面図形の問題として考えたことを合わせる必要があり、その辺りが難しいところだと思います。
(2)はどの位置にいるときの出来事か迷うと思いますが、まず作図してみるとよいでしょう。

問題

ある高層ビルの屋上には，図のような直径７ｍの円周の半分と，長さ２２ｍの直線を組み合わせた形の展望コースがあり，Ｃ地点はＢ地点の真東の方向にあります。身長１８０㎝の父と身長１２０㎝の子どもがこのコース上をＡ地点からＣ地点まで，それぞれ一定の速さで歩きます。ただし，Ａ地点とＢ地点を結ぶ，図の点線は半円の直径です。

（1）ある日，子どもがＡ地点を出発し，父がそのＳ秒後にＡ地点を出発しました。父はＢ地点で子どもを追いこし，さらにそのＴ秒後にＣ地点に到着しました。このときＳ：Ｔ＝１１：７６でした。

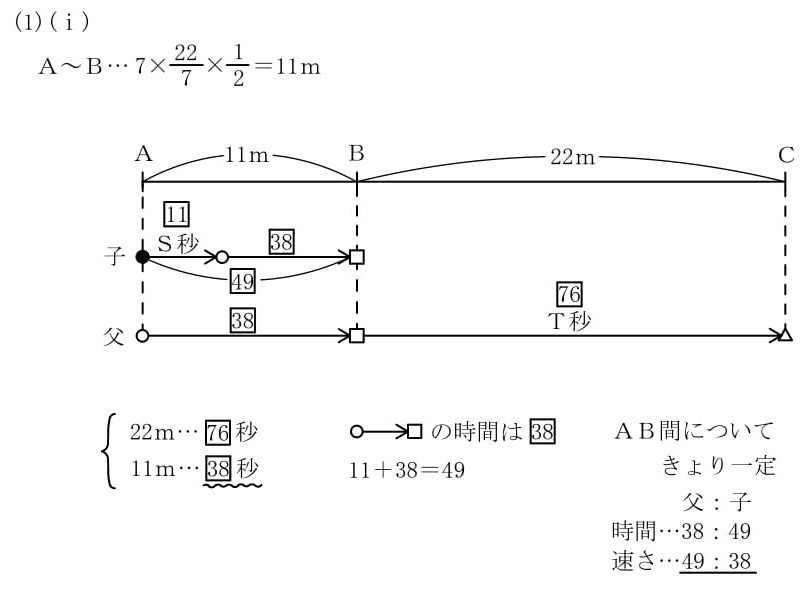
（ⅰ）父と子どもが歩く速さの比を，最も簡単な整数の比で答えなさい。

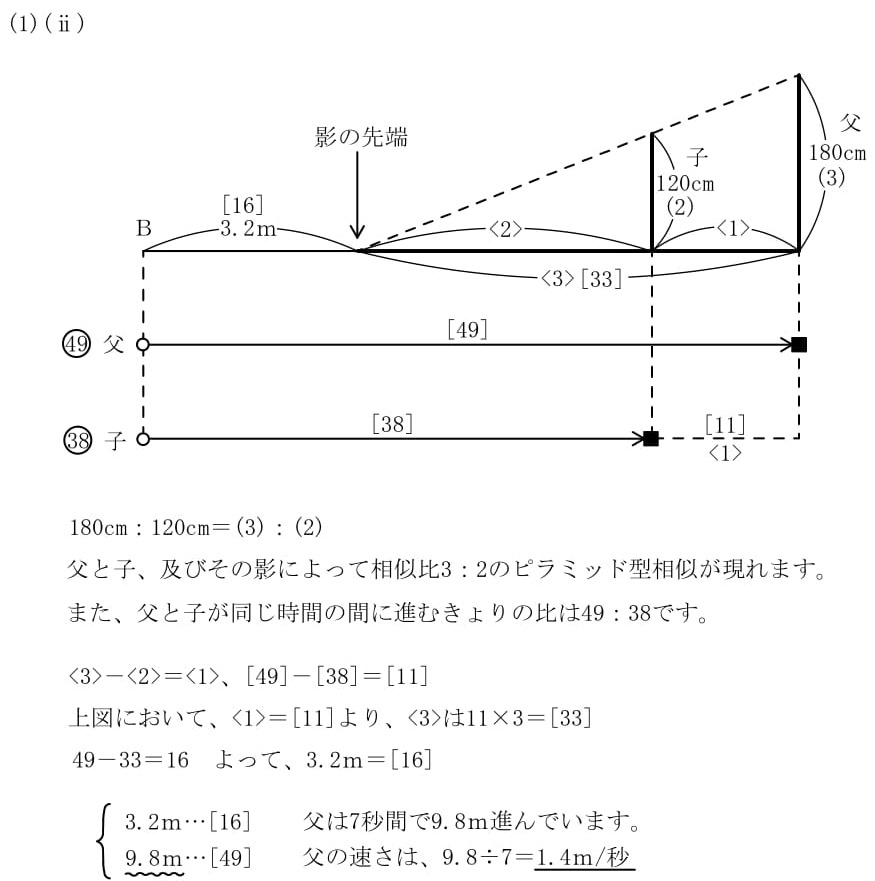
（ⅱ）父が子どもを追いこしてから７秒後に，太陽は真東の方角に出ており，太陽による二人の影の先端がB地点から３.２ｍ真東の地点で重なりました。父の歩く速さは毎秒何ｍですか。

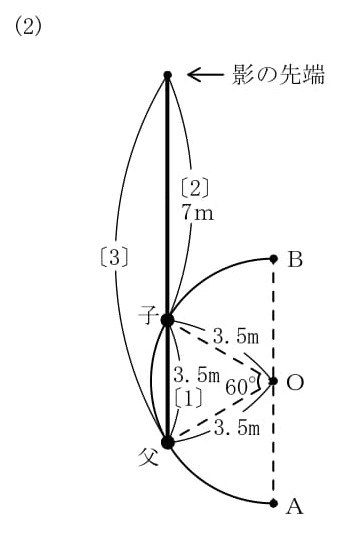
（2）別のある日，子どもがＡ地点を出発し，その後，父がＡ地点を出発しました。前を行く子どもがＢ地点を通過するまでに太陽による二人の影の先端が重なり，そのとき，子どもの影の長さは７ｍでした。影の先端が重なってから何秒後に父が子どもを追いこしますか。ただし，二人が歩く速さは(1)(ⅱ)の速さと等しいものとします。