高槻中学校　2019年（A日程）　大問５（整数・場合の数）

問題

　（1）選ばれた6つの数のうち5つが,1,4,9,16,25のとき,「良い選び方」となるようなもう1つの数を

　　  すべて答えなさい。

（2）,（3）は求め方を,式と言葉を用いて書くこと。

　（2）選ばれた6つの数のうち3つが,1,19,31のとき,「良い選び方」となるような残り3つの数の組は

　　　  何組ありますか。ただし,選ぶ数字の順番は考えません。

　（3）「良い選び方」となるような6つの数の組は全部で何組ありますか。ただし,選ぶ数字の順番は

　　　  考えません。

解説

（1）選ばれた数字をそれぞれ5で割ったときに、1余る数を[1]、2余る数を[2]、3余る数を[3]、

　　  4余る数を[4]、割り切れる数を[0]、と表すことにすると、

　　  1,4,9,16,25はそれぞれ[1],[4],[4],[1],[0]と表すことができます。

　　  つまり、 [0]は5の倍数を表すことになります。

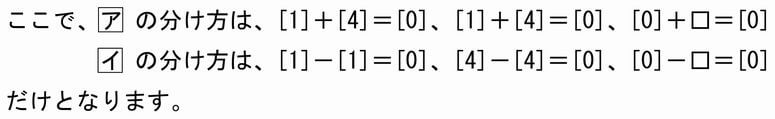
  　　よって、□は[0]より、□＝5,10,15,20,30となります。

（2）1,19,31はそれぞれ[1],[4],[1]と表すことができます。

　　（1）も参考にすると、６つの数は[1],[4],[1],[4],[0],[0]でなければなりません。

　　　ですから、残り3つの数は[4],[0],[0]です。

　　  （詳細な理由：[1]＋[4]＝[0]ですが、[4]－[1]は[0]ではないので、[1]も[4]も2つずつ用意しない

　　　 と差を[0]にすることはできません。また、残り2つの数を[x],[y]とすると[x]と[y]の和も差も[0]

　　　 にするには[x]も[y]も[0]でなければなりません。）

　　  [4]にあたる数は、4,9,14,24,29の5つあります。

　　  [0],[0]にあたる数は5,10,15,20,25,30の6つから2つを選ぶので、6×5÷2＝15組あります。

　　  よって、5×15＝75組

（3）・6つの数が全部[0]である場合…6つの数が5,10,15,20,25,30であるとき→1組

　　  和が[0]になる2つの数は[1],[4]もしくは[2],[3]ですので、

　　  ・6つの数が[1],[1],[4],[4],[0],[0]である場合

　　　  [1]は1,6,11,16,21,26,31の7つあり、[4]は4,9,14,19,24,29の6つあります。

　　 　それぞれ2個ずつ選ぶ場合の数は （7×6÷2）×（6×5÷2）＝315通り　315×15＝4725組

　　  ・6つの数が[2],[2],[3],[3],[0],[0]である場合

　　　  [2]は2,7,12,17,22,27の6つあり、[3]は3,8,13,18,23,28の6つあります。

　　　  それぞれ2個ずつ選ぶ場合の数は（6×5÷2）×（6×5÷2）＝225通り　225×15＝3375組

　　　  よって、1＋4725＋3375＝8101組