洛星中学校　2020年（前期）　大問５（速さ）

問題

ウサギとカメが山のふもとから頂上まで競走をします。

2匹は同時に一定の速さで走り始めましたが,走り始めて2分後にウサギが昼寝を始めてしまい,その48分後にカメが昼寝をしているウサギを追いこしました。

(1)　ウサギとカメの走る速さの比を,もっとも簡単な整数の比で答えなさい。

しばらくしてウサギが起きました。

そのあと,もしウサギがもとの2倍の速さで走れば,3分後にA地点でカメに追いつき,カメより1分24秒早く頂上に着くことができます。

(2)　ウサギが昼寝をしていたのは何分間ですか。

(3)　ふもとからA地点までと,A地点から頂上までの道のりの比を,もっとも簡単な整数の比で答えなさい。

ところが実際には,ウサギはもとの1.2倍の速さで走ったので,カメが頂上に着いたとき,ウサギは頂上から260ｍ手前のところにいました。

(4)　山のふもとから頂上までの道のりは何ｍですか。

解説

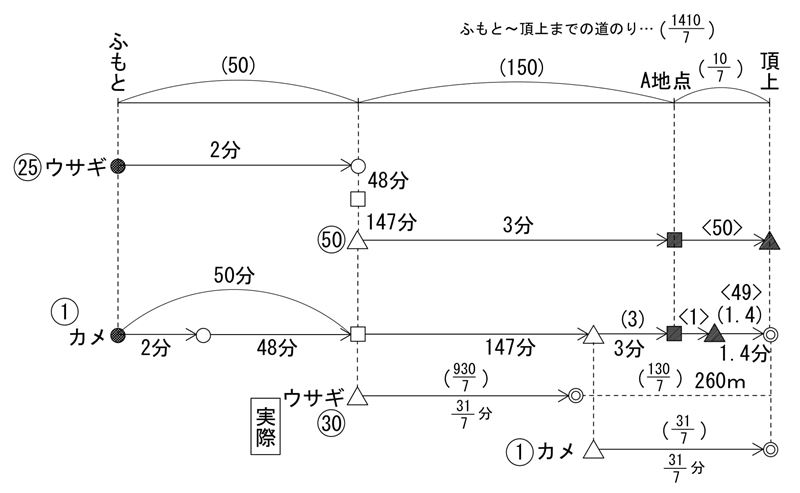
(1) 2+48＝50分　ウサギが2分で走る距離とカメが50分で走る距離が同じで、速さの比は時間の比の逆比となります。

速さの比　ウサギ：カメ＝50：2＝25：1

(2) 速さが2倍になったウサギの速さは、25×2＝50

ウサギが3分で進む距離は50×3分＝(150)

カメが3分で進む距離は1×3分＝(3)

です。

(150)-(3)＝(147)

(147)÷1＝147分

48分＋147分＝195分

(3) 1分24秒＝1.4分　1×1.4分＝(1.4)　1×50分＝(50)

■～◎区間においては時間一定、ウサギとカメの進んだ距離は速さの比と同比です。

距離　ウサギ：カメ＝<50>：<1>

<50>-<1>＝<49>

(1.4)はこの<49>に相当しますので、<50>は(1.4)×50/49＝(10/7)に相当します。

ふもと～A地点までの距離は(50)+(150)＝(200)

A地点から頂上までの道のりは(10/7)より、

(200)：(10/7)＝1400：10＝140：1

(4) 速さが1.2倍になったウサギの速さは、25×1.2＝30

ウサギが起きてからカメが進んだ距離は(3)+(10/7)＝(31/7)で、かかった時間は

(31/7)÷1＝31/7分

その間にウサギが進んだ距離は、30×31/7分＝(930/7)

(150)+(10/7)-(930/7)＝(130/7)…これが260ｍに相当します。

ふもとから頂上までの距離は(50)+(150)+(10/7)＝(1410/7)ですので、

260÷130/7×1410/7＝2820ｍ