- 075-463-4050平日 15:00~22:00
土曜 13:00~18:00 - お問合わせ
- 075-463-4050平日 15:00~22:00
土曜 13:00~18:00 - お問合わせ
東山中学校 2016年 前期 大問6(数と計算)
問題文に従って数を足していく作業をするのですが、そのこと自体は難しくありません。
足していった結果、どのような数が残るのかを考えることが大切です。
問題
0,1,2,3,4,5,6,7,8,9の数字の書かれたカードが1枚ずつ10枚あります。
この10枚のカードから5枚を選び,右の図の(ア)から(オ)の位置に1枚ずつ並べ5けたの整数をつくります。
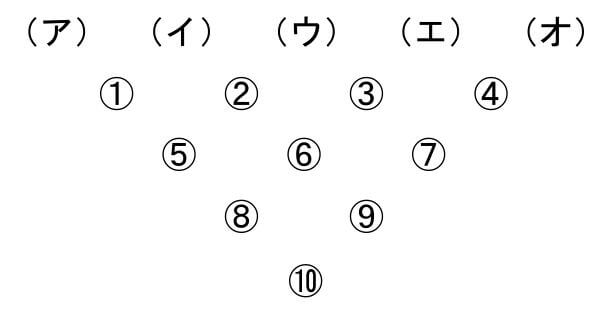
次に, (ア)にある数と(イ)にある数との和を①に書きこみます。
(イ)にある数と(ウ)にある数との和を②に書きこみます。
(ウ)にある数と(エ)にある数との和を③に書きこみます。
(エ)にある数と(オ)にある数との和を④に書きこみます。
①にある数と②にある数との和を⑤に書きこみます。
②にある数と③にある数との和を⑥に書きこみます。
③にある数と④にある数との和を⑦に書きこみます。
⑤にある数と⑥にある数との和を⑧に書きこみます。
⑥にある数と⑦にある数との和を⑨に書きこみます。
⑧にある数と⑨にある数との和を⑩に書きこみます。
これで,和を書きこむ作業は終わります。
ここで,⑩に書いた数のことを,(ア)から(オ)に並べられた5けたの整数の【最後の和】とよぶことにします。
例えば,23456の場合は,
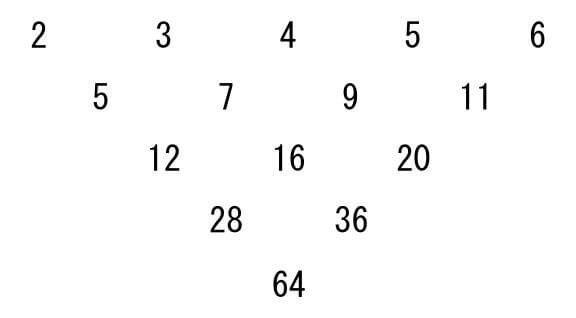
「23456の【最後の和】は,64」となります。
このとき,次の問いに答えなさい。
(1) 28675の【最後の和】を求めなさい。
(2) 最も小さい【最後の和】を求めなさい。
(3) 最も大きい【最後の和】をもつ5けたの整数の中で,最も大きい整数と最も小さい整数との差を求めなさい。
解説
(1)
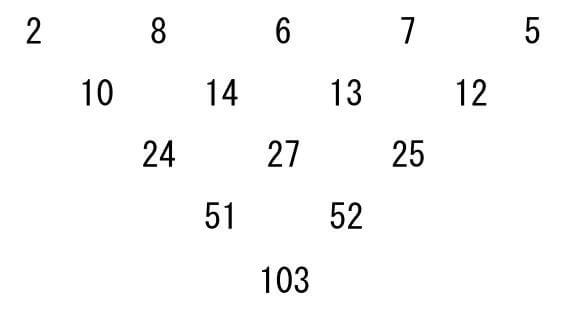
以上より、103となります。
(2) 5けたの整数をabcdeとすると、順に作業をすると和は以下のようになります。
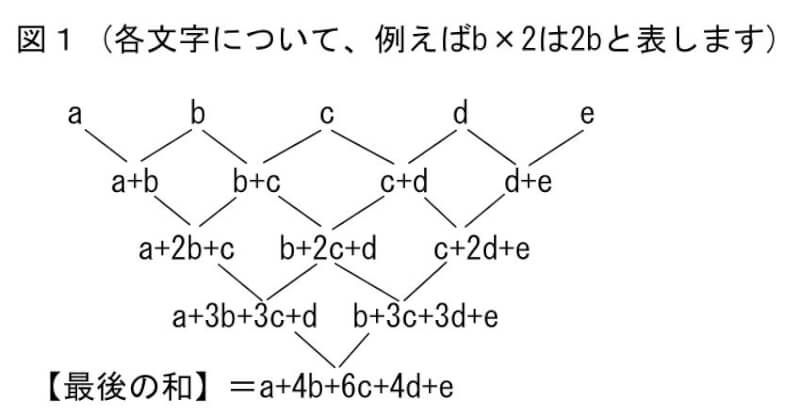
和を小さくするには5枚のカードは最も小さいものから、つまり0,1,2,3,4を使用します。
【最後の和】では、cが6倍されることになるのでcは最も小さく、0になります。
b,dは4倍されることになりますので、b,dは次に小さい1,2です。(どちらが1でも構いません)
a,eは残りの3,4になります。(これもどちらが3でも構いません)
よって、
3+1×4+0×6+2×4+4=19
(3) 【最後の和】が最も大きいのは5,6,7,8,9を使用するときで、
c→b,d→a,eの順に大きい数をあてはめます。
最大の数=68975 (【最後の和】=6+8×4+9×6+7×4+5=125)
同じ【最後の和】(125)を持つ最小の数は、最大の数のaとe、bとdを入れかえた数です。
最小の数=57986
よって、
68975-57986=10989





