洛星中学校 2017年 前期　大問6(数と計算)

問題

　次の問いに答えなさい。

（１）　正三角形の板をすきまなく並べて平行四辺形をつくり、2本の対角線のうち長い方の線で切断します。

　　図１は、5列3段に並べたときで、切断された正三角形の板の枚数は14枚です。

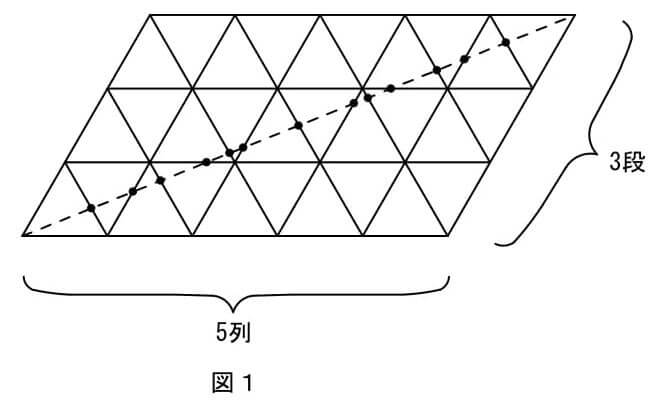
（ア）　9列4段に並べたとき、切断された正三角形の板の枚数は何枚ですか。

（イ）　41列17段に並べたとき、切断された正三角形の板の枚数は何枚ですか。

（ウ）　189列84段に並べたとき、切断された正三角形の板の枚数は何枚ですか。

（２）　正三角形の板をすきまなく並べて平行四辺形をつくり、2本の対角線のうち短い方の線で切断します。

　　図２は、5列3段に並べたときです。

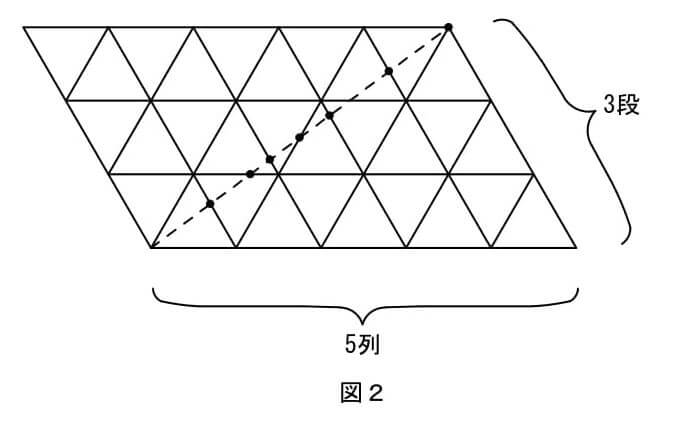
833列476段に並べたとき、切断された正三角形の板の枚数は何枚ですか。

解説

 図１を、正三角形2枚からなるひし形を正方形になるように、以下のように変形させてみます。

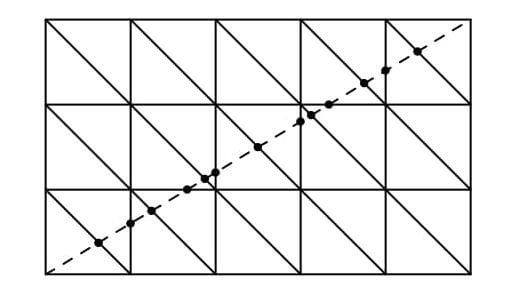
このようにしても切断される枚数には影響しません。

正方形が1枚切断されるごとに三角形は2枚切断されますので、

正方形が何枚切断されたかを求め、その数を2倍するとよいことになります。

ここで、正方形をx列y段の長方形になるよう並べたとき、対角線で切断される正方形の枚数は

「x+y－(xとyの最大公約数)　」

で求められます。

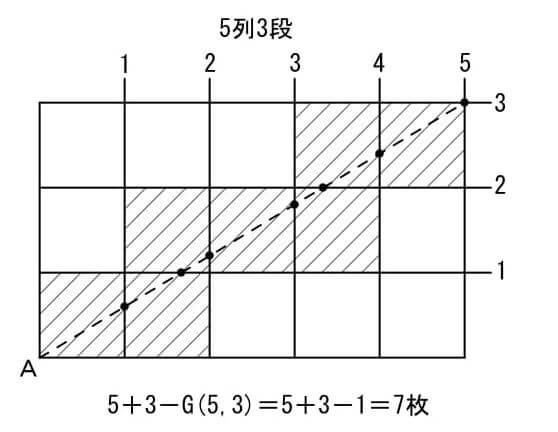
 【理由】

点Ａから対角線を引くとき、タテ・ヨコの線に到着する度に正方形が切断されます。

よってタテ・ヨコの線の本数の合計＝x＋yが関係しているのですが、もう一つ重要なことがあります。

それは、正方形の頂点を通る場合はタテとヨコの線を同時に横切るが、

切断される正方形は一枚だということです。

このため、出発点を除く正方形の頂点に到着する回数（xとyの最大公約数）ぶんを引く必要があり、

先述の式になります。

(１)　

(ア)　9＋4－G(9,4)＝9＋4－1＝12　

　　  12×2＝24枚

(イ)　41＋17－G(41,17)＝41＋17－1＝57

　　　57×2＝114枚

(ウ)　189＋84－G(189,84)＝189＋84－21＝252

　　　252×2＝504枚

　　　もしくは189列84段は（ア）の9列4段の21倍であることを利用して、24×21でも求められます。

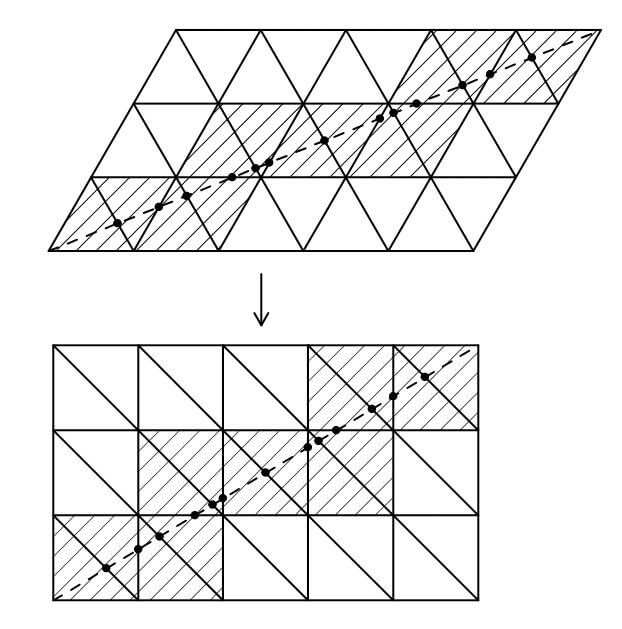
(２)　図２を例にし、下図の太線部分について考えます。

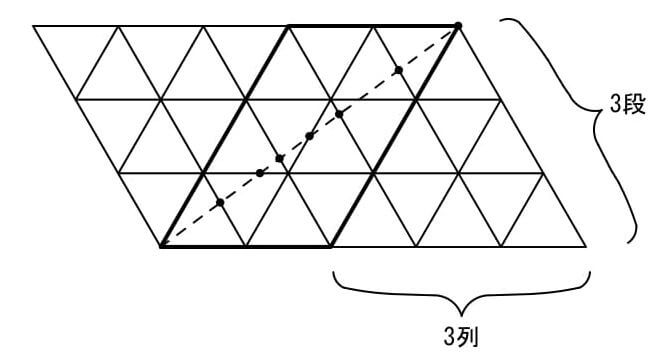
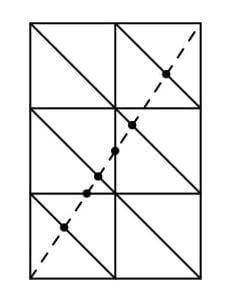
太線部分は、「正方形を2列3段の長方形になるよう並べた形」に変形させることができます。

これで(１)と同じ解き方ができます。

2列というのは、上図のように3段に並べた場合は3列減ることから、5－3＝2、で求めることができます。

833列476段の場合、

833－476＝357列、より357列476段の長方形に置き換えられます。

357＋476－G(357,476)＝357＋476－119＝714

714×2＝1428枚、となります。