洛南高等学校附属中学校　2021年　大問4（割合と比、食塩水）

問題

3つの容器Ａ,Ｂ,Ｃにはそれぞれ濃度の異なる食塩水がいくらか入っています。

入っている食塩水の重さは,Ａが最も軽く,Ｃが最も重いです。さらに次のことがわかっています。

・Ａ,Ｂ,Ｃに入っている食塩の重さは同じです。

・Ｃから,Ｂに入っている食塩水と同じ重さの食塩水を取り除くと,Ｃに残る食塩の重さは35gとなります。

・Ｂから,Ａに入っている食塩水と同じ重さの食塩水を取り除くと,Ｂに残る食塩の重さは56gとなります。

・Ｃから,Ａに入っている食塩水と同じ重さの食塩水を取り除くと,Ｃに残る食塩の重さは63gとなります。

このとき,次の問いに答えなさい。

(1)　（Ａに入っている食塩水の重さ）：（Ｂに入っている食塩水の重さ）を,最も簡単な整数の比で表しなさい。

(2)　Ａに入っている食塩の重さは何gですか。

(3)　Ａ,Ｂ,Ｃに入っている食塩水をすべて混ぜ合わせたときにできる食塩水の濃度は,Ｃに入っている食塩水の濃度の何倍ですか。

解説

食塩水の公式は、「食塩＝食塩水×濃さ」です。

Ａ,Ｂ,Ｃに入っている食塩の重さは同じなので、食塩水の重さと濃さの間で反比例の関係が生じます。ここがポイントです。

食塩水の重さは、Ａ＜Ｂ＜Ｃで、濃さはＡ＞Ｂ＞Ｃです。

ここで、食塩水の重さの線分図を描きます。

問題文が指している以下の部分を線分図に書きこんで整理します。

・Ｃから,Ｂに入っている食塩水と同じ重さの食塩水を取り除くと,Ｃに残る食塩の重さは35gとなります。→※１

・Ｂから,Ａに入っている食塩水と同じ重さの食塩水を取り除くと,Ｂに残る食塩の重さは56gとなります。→※２

・Ｃから,Ａに入っている食塩水と同じ重さの食塩水を取り除くと,Ｃに残る食塩の重さは63gとなります。→※３

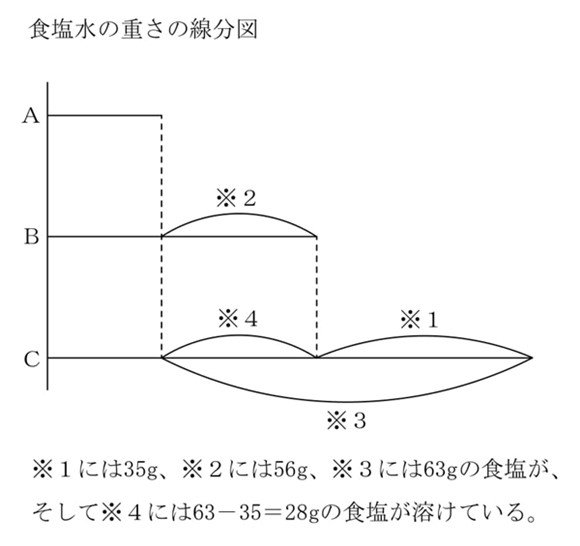
※４の部分は食塩水Ｃについて、※３の部分から※１の部分を引いた重さです。

※２、※４の部分を見ると、同じ重さの食塩水中にＢは食塩が56g溶けているのに対し、Ｃは28g溶けていることがわかります。

このことから、ＢとＣの濃さの比が56：28＝2：1であることがわかります。

よって、ＢとＣの食塩水の重さの比は、逆比が起こり、1：2となります。

また、食塩水の重さを比の数値で書き加えると以下のようになります。

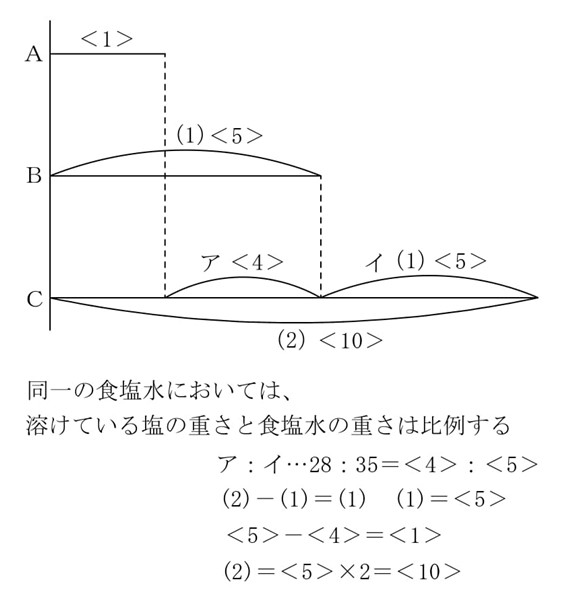
(1)

線分図より、1：5

(2)

Ｃには35×2＝70gの塩が溶けています。

よって、Ａにも70gの塩が溶けています。

(3)

Ａ,Ｂ,Ｃを全て混ぜ合わせた濃さ

（70×3）÷（＜1＞＋＜5＞＋＜10＞）＝[13.125]

Ｃの濃さ

70÷＜10＞＝[7]

[13.125]÷[7]＝1.875倍