2019-02-12
- 075-463-4050平日 15:00~22:00
土曜 13:00~18:00 - お問合わせ
- 075-463-4050平日 15:00~22:00
土曜 13:00~18:00 - お問合わせ
入江塾は、京都市の「育星舎」の中学受験専門塾で、中学受験をする小学生を対象とした進学塾です。無理のない楽しい中学受験で志望校合格を目指します。本部の北野教室(北野白梅町、円町)を中心に出町教室でも開講中。洛星、西京、洛北、東山、同志社、京都女子、同志社女子など毎年多くの中学に合格している実績があります。
西大和学園中学校 2016年 大問2(3)(4) (平面図形)
大問2は平面図形の小問が4つ出題されましたが、それぞれが難しめの問題です。
ここではその中の2問を取り上げます。
こうした問題に対応できるように、普段からしっかり図形の練習をしておく必要があります。
問題


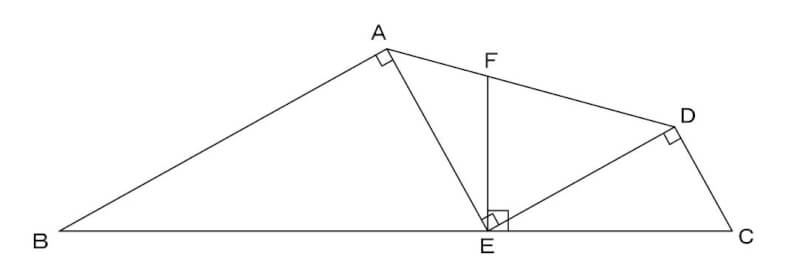
解説
(3) まずAIに直線を引きます。
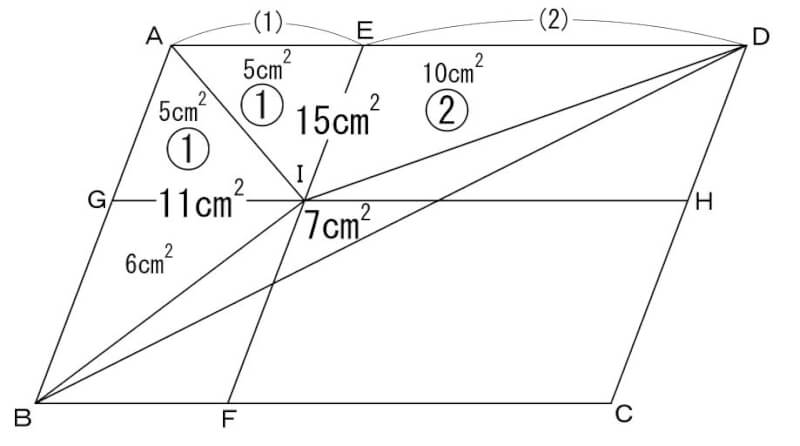
三角形ABDの面積は66÷2=33㎠です。
また、平行四辺形ABFEの面積は平行四辺形ABCDの3分の1なので66÷3=22㎠で、
三角形ABIの面積はその半分なので22÷2=11㎠となります。
三角形AIDの面積は33-(11+7)=15㎠です。
三角形AIEと三角形EIDの面積比は1:2なので三角形AIEの面積は5㎠となります。
三角形AIEと三角形AGIは面積が等しいので三角形AGIの面積も5㎠、
三角形GBIの面積は11-5=6㎠です。
三角形AGIと三角形GBIの面積を比較し、AG:GB=5:6
(4) 辺BAとCDを延長し、交わった点をGとします。
AE=EDで、AEとGDは平行、AGとEDは平行なので四角形AEDGは正方形です。
さらにEFを延長し、AGと交わった点をHとすると、
三角形AFHと三角形DEFはチョウチョ型相似となり、相似比は3:4です。

三角形EAHと三角形EDCは合同で、三角形EAHと三角形BAEは相似(相似比3:4)です。

関連記事





