灘中学校　2021年　第一日　問５（整数）

割り算の余りに関する問題で、問題文は短いですが複雑な思考を要求されます。
整数Ａを15で割った余りがＢであるとき、Ａ×Ａを15で割った余りと、Ｂ×Ｂを15で割った余りは等しいということを利用するのが好ましいのですが、その事実に行きつくかどうかは日頃の数字に対する考えの深さによって決まるでしょう。

問題

Ａは２桁の整数で,Ａ×Ａを15で割ると1余ります。このようなＡは全部で□個あります。

Ａを15で割った余りをＢとし、Ａ×Ａを15で割った余りとＢ×Ｂを15で割った余りが等しい（※1）ことを利用して解きます。

Ｂは14以下の整数なので、14までについて調べます。

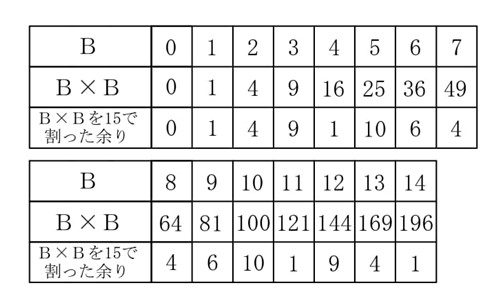
上表より、Ｂ×Ｂを15で割った余りが1になるのはＢ＝1,4,11,14のときです。

Ａは15の倍数＋1、15の倍数＋4、15の倍数＋11、15の倍数＋14のいずれかです。

2桁の整数は10～99までの90個で、90÷15＝6あまり0であるため、どれもちょうど6個ずつある（※2）ことがわかります。

よって、6×4＝24個

（補足）

※1

面積図で考えます。

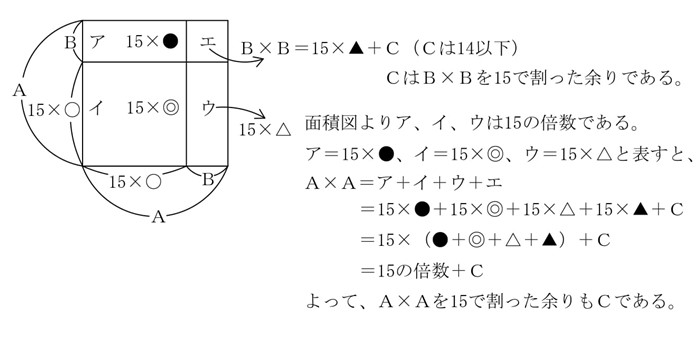
※2

全て書き出すと以下のようになります。

Ｂ＝1のとき、Ａ＝16,31,46,61,76,91

Ｂ＝4のとき、Ａ＝19,34,49,64,79,94

Ｂ＝11のとき、Ａ＝11,26,41,56,71,86

Ｂ＝14のとき、Ａ＝14,29,44,59,74,89