甲陽学院中学校（2020年　第一日）　大問３（平面図形）

問題

６つの角がすべて120°の六角形ABCDEFがあり、辺の長さは図のようになっています。この六角形を辺AFに平行な直線PQによって２つの五角形APQEFとPBCDQに分けると、その２つの五角形の周の長さが等しくなりました。

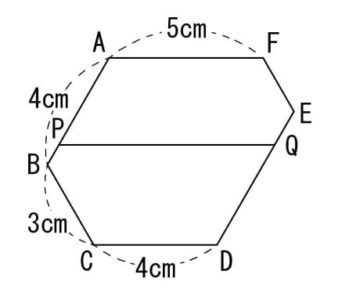
（１）APの長さを求めなさい。

（２）五角形APQEFと五角形PBCDQの面積の比をできるだけ簡単な整数の比で表しなさい。

解説

辺AB、CD、EFを延長して大きな三角形を作り、三角形GHIとします。

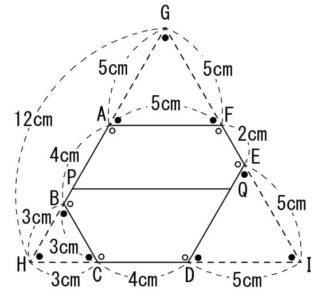
六角形ABCDEFの外角は全て60°なので、六角形ABCDEFに正三角形を３つ付け足した形になり、同時に、三角形GHIも正三角形です。

AG=5ｃｍ、BH=3ｃｍより、GHの長さは5＋4＋3＝12ｃｍです。

以上より、CH=3ｃｍ、DI=12－(3＋4)＝5ｃｍ、

また、

EI=5ｃｍ、FG=5ｃｍ、EF＝12－(5＋5)＝2ｃｍ

とわかります。

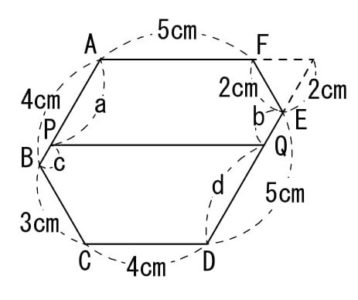
上図のように各部分の長さをa,b,c,dとし、五角形APQEFとPBCDQの周の長さが等しいことを式にします。

a＋PQ＋b＋2＋5＝c＋3＋4＋d＋PQ

a＋b＋7＋PQ＝c＋d＋7＋PQ

a＋b＝c＋d

a＋b＋c＋d＝４＋５＝9ｃｍなので、

a＋b＝９÷２＝４.５ｃｍ…①

a－b＝２ｃｍ…②

①＋②の式を作ると、

（a＋b）＋（a－b）＝a×２＝６.５

a＝６.５÷２＝３.２５ｃｍ

（２）相似の面積比で考えます。

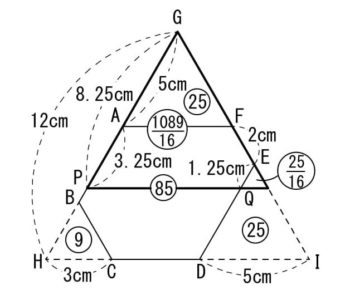
相似比の2乗が面積比ですので、正三角形GHIの面積（比）を１２×１２＝１４４とします。

ここからスミにある正三角形３つの面積（比）を引きます。

１４４－（５×５＋３×３＋５×５）＝８５…六角形ABCDEFの面積（比）

辺GPを一辺とする正三角形（図の太線部）の面積（比）は、５＋３.２５＝８.２５＝３３/４ｃｍより、３３/４×３３/４＝１０８９/１６

正三角形GAFの面積（比）は、５×５＝２５

辺EQを一辺とする正三角形の面積（比）はb＝３.２５－２＝１.２５＝５/４ｃｍより、５/４×５/４＝２５/１６

よって、五角形APQEFの面積（比）は、１０８９/１６－２５/１６－２５＝４１.５

五角形PBCDQの面積（比）は８５－４１.５＝４３.５

五角形APQEF：PBCDQ＝４１.５：４３.５＝８３：８７