東山中学校　2018年前期Ｂ　大問７（規則性）

「継子立て」の問題です。

普通に作業していくとかなり大変ですが、ある事実に着目するとすっきり解けます。

問題

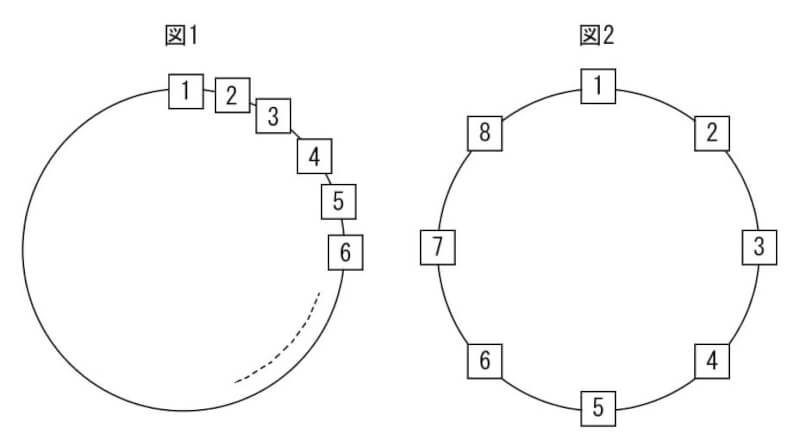
1から順に整数が書かれているカードがあります。図1のように、これらのカードが1から順にある整数まで時計回りで

円形に並んでいるものを考えます。ここから、1のカードを最初に取り除き、時計回りで1つおきにカードを取り除いて

いき、最後に残るカードについて考えます。例えば、図2のように8のカードまで並んでいるとき、1、3、5、7、2、6、4

の順でカードを取り除き、最後に残るのは8のカードになります。

このとき、次の問いに答えなさい。

（1）16のカードまで並んでいるとき、最後に残るカードに書かれている整数を求めなさい。

（2）2018のカードまで並んでいるとき、最後に残るカードに書かれている整数を求めなさい。

（1）周ごとに残っているカードを書き出すと次のようになります。

よって、16が最後に残ります。

（2）（1）のときのようにカードの残り枚数が2枚、4枚（2×2枚）、8枚（2×2×2枚）、16枚（2×2×2×2枚）のように

2だけを何個かかけた数のときは、一番後ろに置かれているカードが最後まで残ることがわかります。

2018のカードまで並んでいる場合、2だけを何個かかけていった数を考えると2018までの中で一番近いものは

2×2×2×2×2×2×2×2×2×2＝1024です。

よって、1024枚のカードが残るときを考えます。

ここまでに2018－1024＝994枚取り除き、最後に取り除いたカードは、

1＋2×（994－1）＝1987

ですのでこの次に取り除くカードは1989です。

1989を先頭に考えると1988が一番後ろに置かれていることになりますので、1988が最後に残ります。