2022-02-09
- 075-463-4050平日 15:00~22:00
土曜 13:00~18:00 - お問合わせ
- 075-463-4050平日 15:00~22:00
土曜 13:00~18:00 - お問合わせ
入江塾は、京都市の「育星舎」の中学受験専門塾で、中学受験をする小学生を対象とした進学塾です。無理のない楽しい中学受験で志望校合格を目指します。本部の北野教室(北野白梅町、円町)を中心に出町教室でも開講中。洛星、西京、洛北、東山、同志社、京都女子、同志社女子など毎年多くの中学に合格している実績があります。
洛南高等学校附属中学校 2020年 大問2(5)(平面図形)
図はシンプルですが奥深く、補助線を引く力が必要です。
ひらめきを要するので試験場ではわからなければ飛ばし、時間を取られないようにせねばなりません。
豊富な問題経験があればある程度解き方の予想を立てやすくなります。
問題
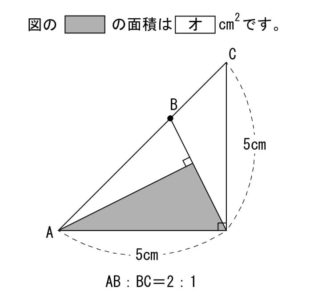
解説
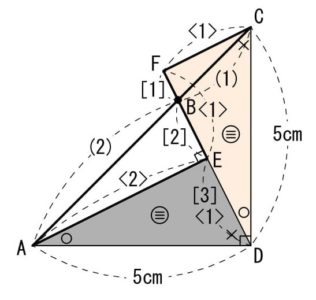
図のように点D、Eをとり、CからAEと平行に線を引きます。
そして、DBを延長した線との交点を点Fとします。
図中のように〇と×がそれぞれ同じ角度となり、一辺とその両端角が等しいので三角形ADEと三角形DCFは合同となります。
また、太線部の三角形AEBと三角形CFBは相似で、相似比が2:1です。
これより、AE:CF=<2>:<1>で、DEの長さは<1>なので、<2>-<1>=<1>よりEFの長さも<1>です。
EB:BF=[2]:[1]で、EF=[3]=<1>より、DEの長さは[3]です。
これらを元に高さが等しい三角形の考え方で面積比を表すと以下のようになります。
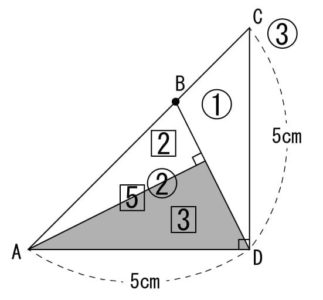
5×5÷2=12.5㎠
12.5×2/3×3/5=5㎠
別解
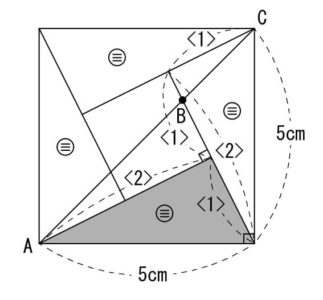
更に線を足すと上図のようになります。
合同な直角三角形が正方形を囲んで、大きな正方形になっています。
この図はよく出題されるものなので、経験したことのある人も多いでしょう。
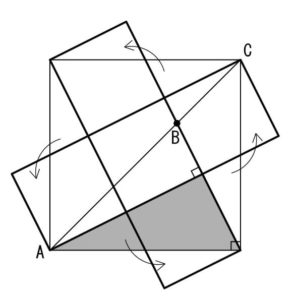
太線部の合同な正方形5つに変形します。
影の部分はそのうちの一つです。
5×5÷5=5㎠





