算数の学習にてポイントを押さえる大切さ

１．指導内容には一つ一つ意味があります

算数の指導方法には説明の仕方に一つ一つ根拠があるのですが、長期的な視野で見て効果を見込んでいるものもあり、一見なぜこんな遠回りなやり方をするのだろうという風に感じてしまう生徒や保護者さんがいらっしゃると思います。

実際、こうした方が早いなどの声を生徒からよく聞きますし、私も時には（うん、そうだよね～、式一発で済むし、わかるならそのほうがいいかもね）などと心の中で呟いています。

ただ、今後の一連の流れに沿った算数の学習をするためには、公式へのあてはめや、ダイレクトに解答を求める方法では応用が利かないことが多いんですよね。

手軽に答えを求めることにこだわってしまい、少し問題の性質が変わっただけで先に進めなくなるということがそういうところから起こってきます。

一つ言っておきますと、何も私は自分に合った方法を探すことを否定しているわけではありません。

私自身受験生の時代には色んな方法で答えを出そうとよく考えました。

無茶苦茶な方法で答えが出るか試したこともありました。

自分なりの方法で算数を攻略しようという気概が、思考力や数感覚を養うことの一役を買うことは確かです。

ただ、それはやるべき事以外のところで、半ば趣味的に行うべきものであり、大筋は習ったことを忠実に自分の考え方に組み込んで定石としていくことが大切であるように思います。

２．図を描くことの意味

普段、計算の順序線を引くように言ったり、線分図・面積図をしっかり描くようにと伝えているのは、ただ単に目の前の問題に対して解く方法を指定しているだけではありません。

そうした道具を使いこなすことでどんな問題にも対応できる準備をしておきなさいという意図があってのことです。

割合や、図形を含む比の問題に関しては、入江塾独自のボックスというものを用いてできるだけ解答への道筋のパターンを統一しています。

単元の始めには、初歩的な、線分図や道具を使わずにあっさりと解ける問題が存在します。

しかし、そのような場合でも解説プリントには図を描いていますし、その方法で授業でも説明をします。

３．割合という分野をどのように捉えるか

例：1200円の6分の5は何円ですか？

解説：

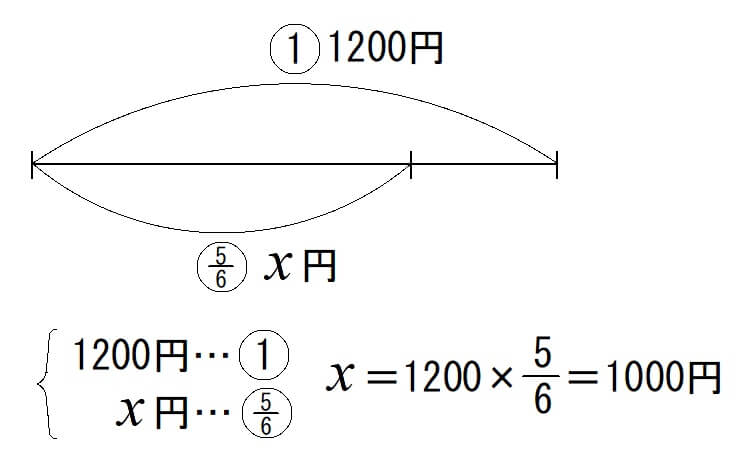
この問題は割合の問題ですが、分数の考え方を用いると1200円を6つに分けた5つ分だと考えることができます。

ですので、1200÷6×5という式を立てても正解なのです。

ですが、分数はあくまで分数の計算という狭い範囲の枠にとどまります。

その一方で、割合は正比例の考え方を多分に含んでいます。

この正比例の考え方は中学受験の軸になるものです。

つまり、正比例の考え方まで含めて理解すると、幅が広がるということですね。

割合をきちんと理解できれば多くの文章題が解ける

割合の考え方は損益算、食塩水、図形と比、速さなどその考え方を用いる範囲は多岐にわたります。

それを同じ一つの理屈でわかるようにしよう、その方がスッキリして整理しやすい、というのが入江塾の考え方です。

塾生には、割合に関する問題は特定の手順で解くように教えています。

それが公式を覚える手間を極力省いたり、単元の本質を理解するための最善手だと考えています。

４、５年生の生徒は線分図などをしっかり描きつつ、ボックスの使い方を身につけましょう。

６年生はその理屈を生かして、計算方法を更に工夫してみましょう。

複雑な問題になっても同じ考え方で解けるということがわかってくると思います。

４．相反する考え方の存在

正比例と対になる反比例（逆比）

ちなみに、正比例だけでなく、反比例も同じくらい大切です。

反比例は、一方が2倍、3倍になればもう一方は2分の1、3分の1になるものを指します。

この反比例の関係は授業では逆比という形でよく登場します。

例えばAさんが3日で終わる仕事をBさんが行うと2日で終わりましたという場合、一日に行う仕事の量はBさんの方が多いですよね。

この場合、かかる日数と、一定時間に行う仕事の量（仕事量）は反比例の関係です。

かかる日数の比はA：B＝3：2で、仕事量の比は逆比を用いるという事で、A：B＝2：3だということになります。

このような場合は逆比になるということは、該当の単元である仕事算のときにも説明していますが、元を辿れば比を習う最初の時にも説明します。

例：A×3＝B×2　のとき、A：Bは？

この式のAに2を入れ、Bに3を入れたら式が成立することはご覧の通りです。

ひっくり返して入れたらぴったりだね、ということも含めて説明しながら、この式が逆比と関連していることを生徒に浸透させていきます。

概念をきちんと理解して区別する

入江塾の指導方法は単元を体系的に分類した上で、その区別をしやすくしています。

その最低限の区別はしっかり行ってもらいたいなと思います。

例えば、よく考えずに全てを正比例の考えで解こうとすると、仕事算や、速さと比の分野でつまずくことになります。

その辺りの注意点は時折伝えるようにしています。

５．算数の学習目標

ズバリ４、５年生の基礎の学習で最低限何ができるようになるとよいのか？

もちろん志望校によって異なってきますが、全員に共通することは各単元について基本問題レベルのものを習った方法で再現できるようになることです。

と言っても、それがなかなか難しいのですが。

毎週異なる内容を学習する中で、混乱してしまって頭の整理ができなくなることは珍しいことではありません。

そんな中でもこの分野は面積図、こっちは線分図、これは文字式、というように断片的にでも覚えておくようにするとよいです。

避けてほしいのがその週の宿題を消化するために、独自の方法で済ませてしまうこと。

これはそのときはわかった気になったり、中にはずっとそれで通す生徒もいますが、間違いのもとになったり、他の分野に応用がきかない場合が多いです。

その場しのぎになってしまうことが多いんですね。

算数における基礎固めは非常に重要です。

４、５年生の生徒は日々地道に積み重ねていき、6年生の生徒は夏までは未消化分野の習得に努めましょう。

６．まとめ

繰り返しになりますが重要なことをまとめておきます。

・授業で指導には一つ一つ意味があるので、面倒くさがらずに実践しましょう

・その上で自分に合った方法を独自に研究し、持っておくことは悪いことではありません（むしろ推奨）

・指導している方法（線分図や面積図、ボックスの使い方など）は単元の本質、または複数の単元にまたがる大きな考え方に通じます

・我流に走ると応用が利かなくなる可能性大です

・算数においては基礎固めが非常に大切です

入江塾　ソフトな中学受験　京都市の学習塾　育星舎グループ

2019.04.09

中学入試・算数「この一題」

算数の入試問題から一題選び、解説をしています。2024年（令和6年）の問題洛星中学校（2024年前期）…大問６（立体図形）洛南高等学校附属中学校（2024年）…大問６（平面図形）東大寺学園中学校（2024年）…大問４（速さ）高槻中学校（2024年A日程）…大問３（平面図形） 2023年（令和5年）の問題洛星中学校（2023年前期）…大問６（平面図形）高槻中学校（2023年A日程）…大問３（速さ）東山中学校（2023年前期Ｂ）…大問６（水量と体積） 2022年（令和4年）の問題洛星中学校（2022年前期）…大問６（平面図形）洛南高等学校附属中...