洛南附属中学　2024年度　大問６(平面図形)

等積変形と三角形の合同をあわせて考える問題でした。(1)と(2)でやったことを(3)では同じようにして自分で活用できるかがポイントです。

問題

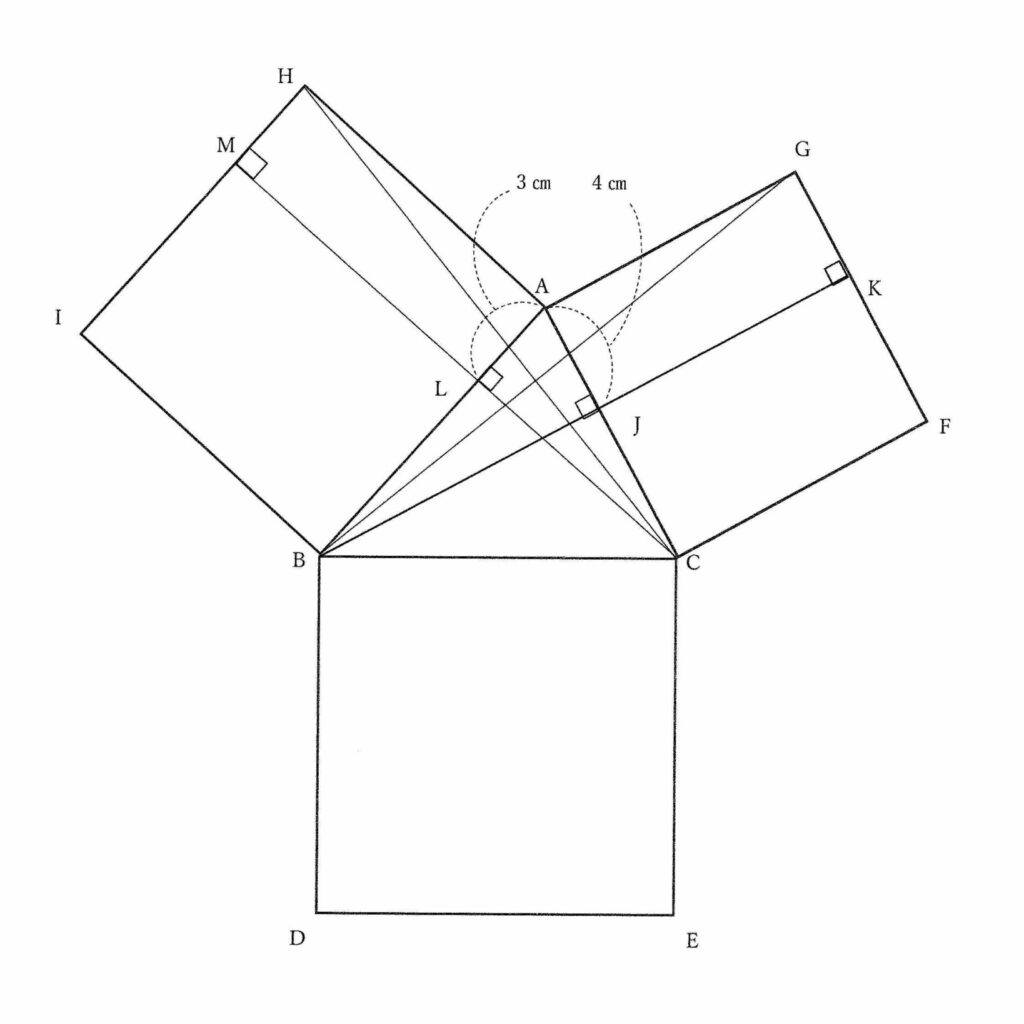
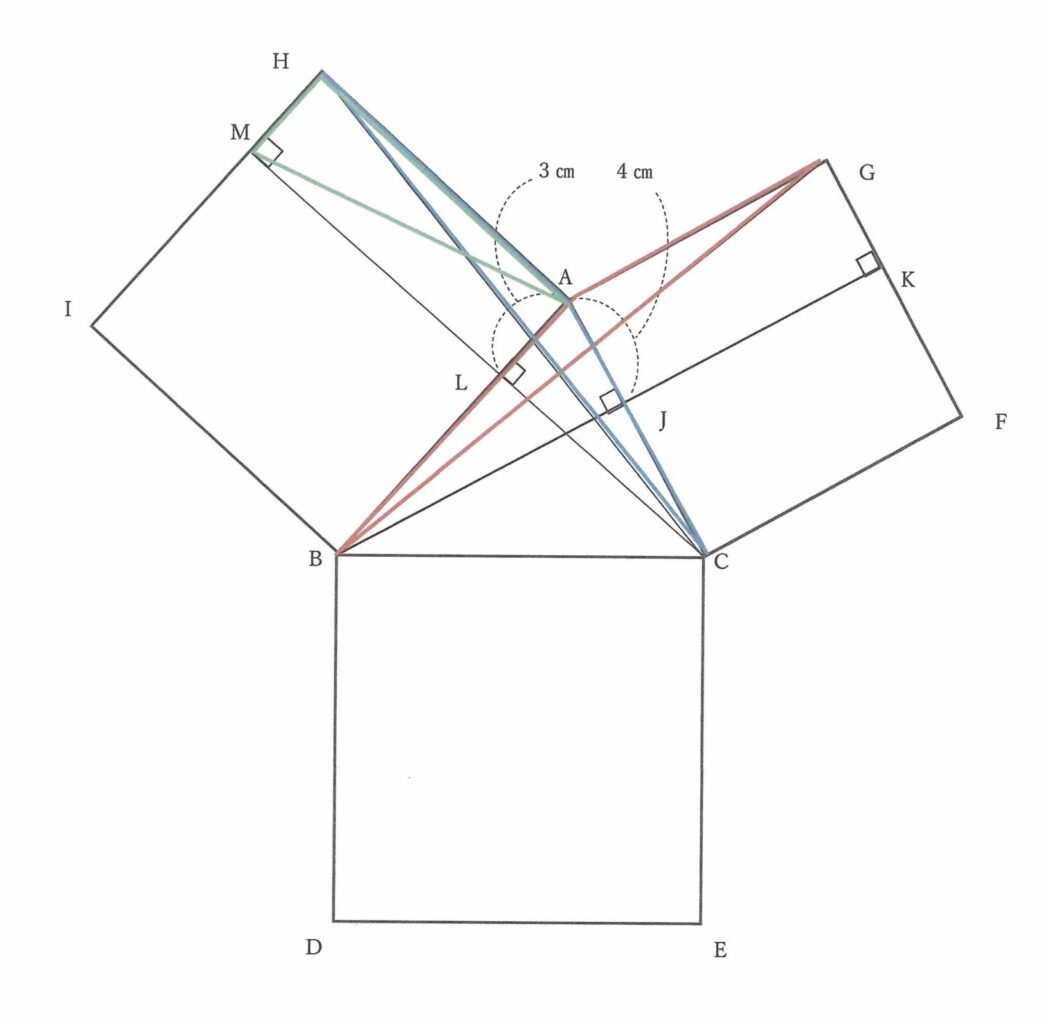
図のように，三角形ABCの各辺に正方形がくっついています。三角形ABGの面積は18㎠で，AJ，ALの長さはそれぞれ4㎝，3㎝です。

このとき，次の図形はそれぞれ何㎠ですか。

(1)四角形AJKG　　　　　　(2)四角形AHML　　　　　　(3)四角形BDEC

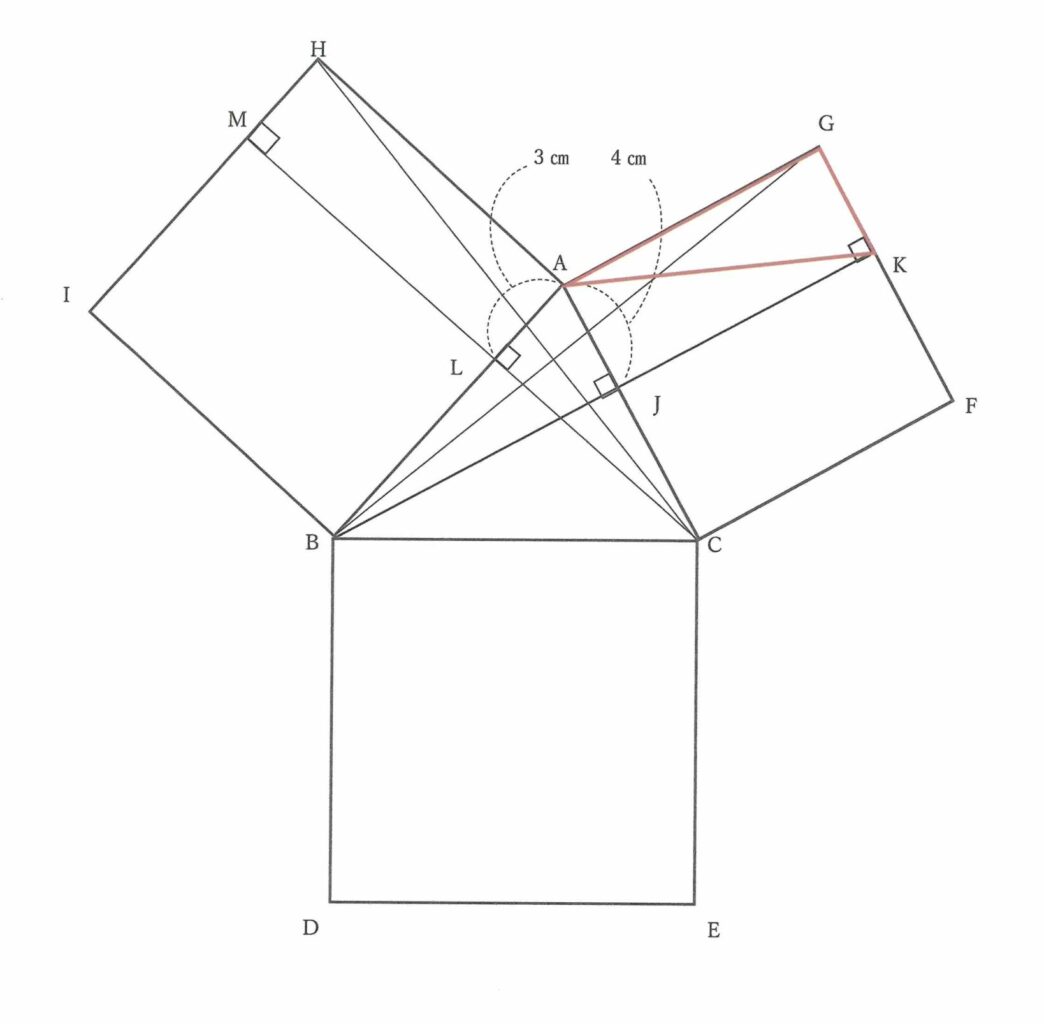
(1)　三角形ABGと三角形AKGは辺AGを共通の底辺とする高さが4㎝の三角形なので，面積が等しい。三角形AKG＝18㎠

よって，四角形AJKGの面積は三角形AKGの2倍で　18㎠　×　2　＝　36㎠

(2)　三角形ABGと三角形AHCは合同（∵　AG＝AC，AB＝AH，∠BAG＝∠BAC＋90°＝∠HAC　）

また，三角形AHCと三角形AHMは辺AHを共通の底辺とする高さが3㎝の三角形なので，面積が等しい。三角形AHM＝18㎠

よって，四角形AHMLの面積は三角形AHCの2倍で　18㎠　×　2　＝　36㎠

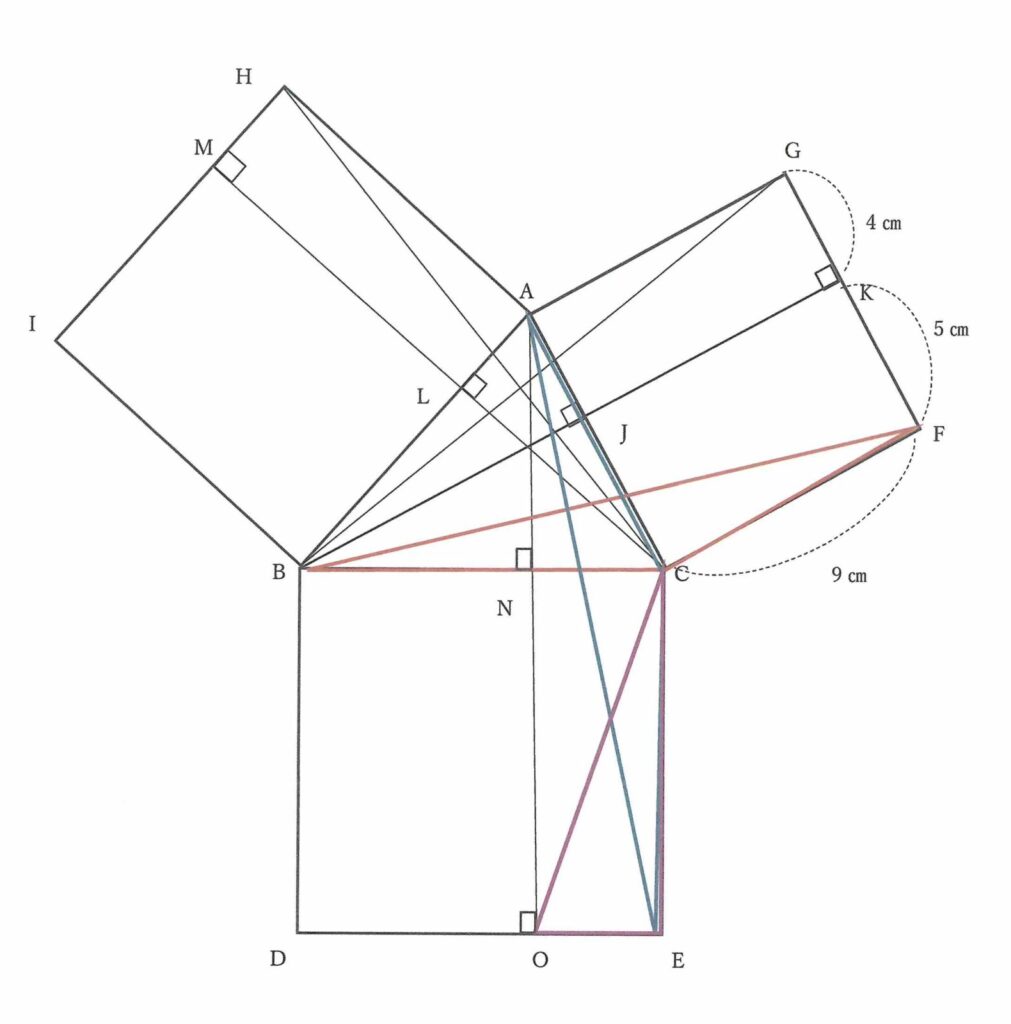
(3)　(1)・(2)より　正方形ACFGの一辺の長さは　36㎠÷４＝9㎝　　正方形AHIBの一辺の長さは　36㎠÷3＝12㎝

点BとFを直線でつなぎ三角形BCFをつくるとその面積は　9㎝×（9－4）÷2＝22.5㎠

また，三角形BCFと三角形ECAが合同　（∵　BC＝EC，CF＝CA，∠BCF＝∠BCA＋90°＝∠ECA　）

ここで点Aから辺BC・辺DHに垂線を下ろした点をそれぞれ点N・点Oとすると三角形ECAと三角形OECは辺ECを共通の底辺とする高さがOEの三角形なので，面積が等しい。三角形OEC＝22.5㎠

四角形OECNの面積は三角形OECの2倍で　22.5㎠　×　2　＝　45㎠

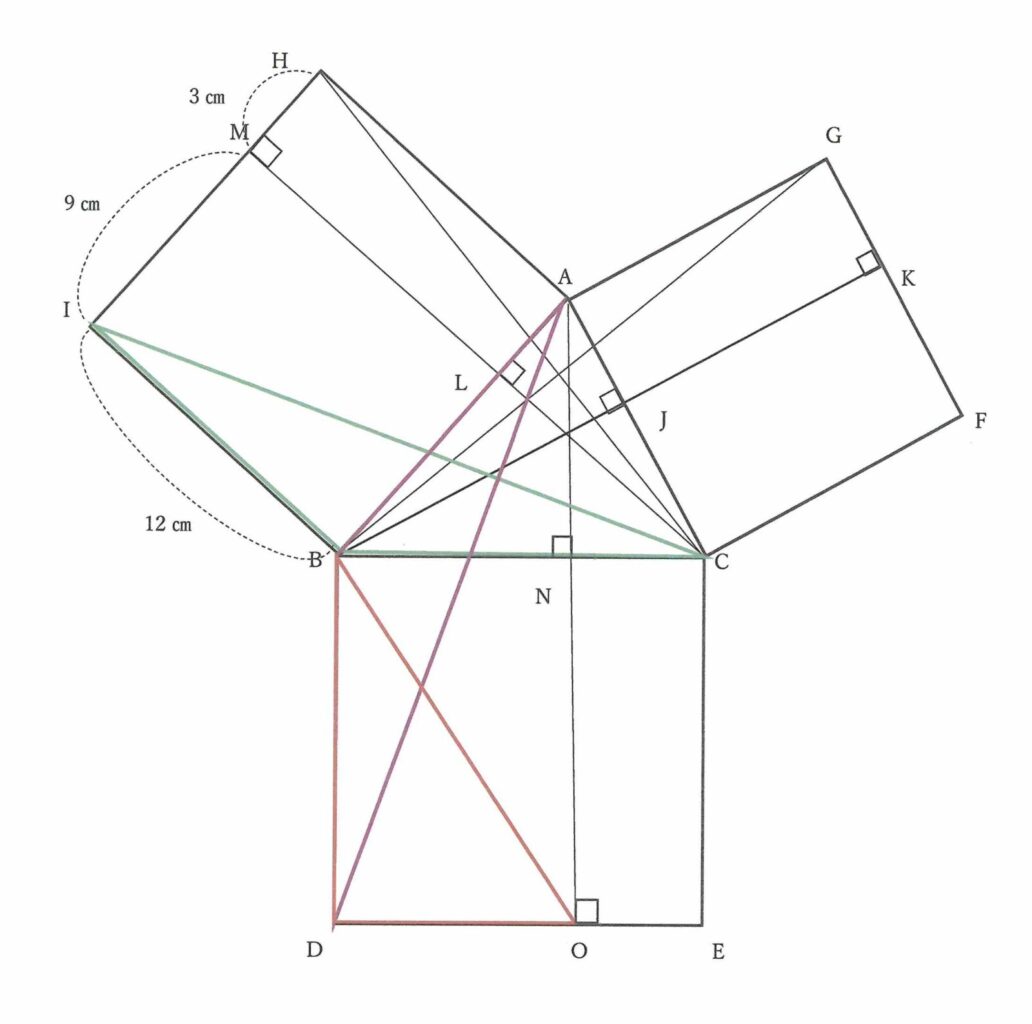
同様にして点CとIを直線でつなぎ三角形BCIをつくるとその面積は　12㎝×（12－3）÷2＝54㎠

また，三角形BCIと三角形BDAが合同　（∵　BC＝BD，BI＝BA，∠CBI＝∠ABC＋90°＝∠DBA　）

そして三角形BDAと三角形BDOは辺BDを共通の底辺とする高さがODの三角形なので，面積が等しい。三角形BDO＝54㎠

四角形BDONの面積は三角形BDOの2倍で　54㎠　×　2　＝　108㎠

よって，四角形BDEC　＝　四角形BDON　＋　四角形OECN　＝　108　＋　45　＝　153㎠